Équilibre d’un pont suspendu
tension
du câble en M1
tension du câble en M2
p.dx.j (j vecteur !) poids supporté par le câble
(En négligeant le poids du câble, p représente le poids au mètre du tablier du pont et du poids utile en charge).
En projetant sur (xx’) on a :
T2cosα2-T1 cosα1 = 0
T2cosα2 = T1 cosα1
La projection horizontale de la force de tension est la même en tout point et on posera :
|
T2cosα2 =T1 cosα1 = T0 (1)
|
En projetant sur (yy’) on obtient la seconde condition d’équilibre :
T2sinα2 – T1 sinα1 = p.dx
-D’où, en se servant de la relation (1) :
En désignant par y = F(x) l’équation du câble
on a : 
Car tanα1 et tanα2 sont les coefficients directeurs des tangentes au câble respectivement en x + dx et en x .
On arrive
à : 
Soit en faisant tendre dx vers 0 :
|
|
-Une double primitivation permet de trouver l’équation du câble :
F'(x) =
+ C1
Ou encore :
F(x) = 
+ C1x+ C2
L’équation du câble est donc :
|
Y =
|
On a
= f et donc 
On en déduit que
Cette formule donne la valeur de la composante horizontale de la tension en tout point du câble.
-La tension est maximum lorsque l’angle α de la tension avec l’horizontale est maximum c’est-à-dire au sommet des piliers porteurs.
On a en ces points la situation suivante :
|
|
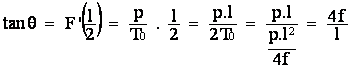
Or
et 
D’où
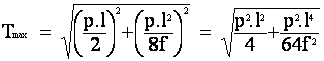
Donc :
|
|
Avec
On a donc
